If the milky way were reduced to the size of an electron, how big would the universe be? This is a simple mathematical question. We only need to know the exact size of the milky way, the electron and the universe to work out the answer to this question based on the ratio between them, as we will discuss below.

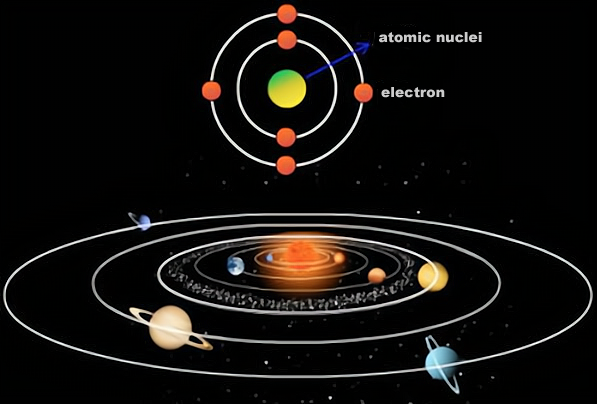
We humans are in the middle of the milky way galaxy and cannot directly see the whole galaxy, but this is not difficult to beat. In the past, scientists using modern observation equipment have determined the size, location, distance and other data of most of the objects in the milky way galaxy, and have inferred the structure, shape and size of the galaxy from this.

As shown above, the main body of the milky way is a 'stellar disk' with a large 'galactic halo' at its periphery, which is very sparse in structure (its main because the structure of the halo is very sparse (the main material is ionised gas, but there are also small amounts of stars, interstellar dust, etc.), what we usually call the size of the milky way refers to the size of the stellar disk, which is about 100,000 light-years in diameter, according to observations.

Electrons are generally treated as a 'dot' because they are so small. Of course, electrons do have a volume, and in order to measure the size of an electron, scientists usually use the method of emitting multiple electrons at a target electron and then using precision instruments to observe the scattering of these electrons to determine the volume of the target electron.

By this method, scientists have come up with the result that the diameter of the electron is no larger than 10^(-18) metres. It is important to note that this is "Not greater than" And not "Equal to", i.e. The diameter of the electron could be smaller than this, so we may as well take the maximum diameter of the electron, which is 10^(-18) metres.

Based on the above data, we can calculate that if the milky way were reduced to the size of an electron, this would be equivalent to reducing the milky way by a factor of about 9.46 x 10^39.

So how big is the universe? In reality, this is a question to which there is no definitive answer.

Due to various constraints (such as the age of the universe, the speed of light, the expansion of the universe, etc.), we can only see a part of the universe, which is also called the "Observable universe", and the size of the whole universe cannot be obtained by actual measurements, but only by theoretical speculation.

In 2006, theoretical physicist leonard sascand, one of the founders of string theory, stated in a paper that the "Bounded infinite universe model" Proposed by the famous physicist stephen hawking and related theories can be calculated as the diameter of the entire universe is about 10 times 10 to the 122nd power of 10 seconds (note: A 1 second gap is approximately 3.26 light years).

What is this concept? Let's put it this way: If the diameter of the universe is x seconds apart, then the number x is 1 followed by y zeros, and the number y is 1 followed by z zeros, and the number z is 1 followed by 122 zeros, which, as you can see, is an extremely large number.

Assuming that the universe is really that big, then for the number "10 of 10 to the 122nd power of 10", a reduction of 9.46 x 10^39 times is just a few dozen fewer zeros after 1. In this case, the universe is still unimaginably large.

Of course, this is only a theoretical estimate, and there is no way of verifying whether this is actually the case, so let's do a more realistic calculation to see how big the 'observable universe' would be if the milky way were reduced to the size of an electron.

The diameter of the 'observable universe' is known to be about 93 billion light years, so shrinking it by a factor of 9.46 x 10^39 would give it a diameter of about 9.3 x 10^(-13) metres.

For comparison, the hydrogen atom is the simplest atom in the universe, and measurements show that a hydrogen atom in the ground state (lowest energy level) is about 1.056 x 10^(-10) metres in diameter, meaning that the shrunken 'observable universe' is not even a hundredth of the diameter of a hydrogen atom. This is so small that even an optical microscope would not be able to observe it, let alone the naked eye.